


Next: Conclusions
Up: Scalable Data Parallel Algorithms
Previous: Maximum Likelihood Estimate
We implement an algorithm for compressing an image of a GMRF texture
to approximately 1 bit/pixel from the original 8 bits/pixel image.
The procedure is to find the MLE of the given image, (e.g. this
results in a total of eleven 32-bit floating point numbers for the 4th
order model). We then use a Max Quantizer, with characteristics given
in [33], to quantize the residual to 1-bit. The quantized
structure has a total of  bits. To reconstruct the image from
its texture parameters and 1-bit Max quantization, we use an algorithm
similar to Algorithm 2. Instead of synthesizing a
texture from Gaussian noise, we begin with the 1-bit quantized array.
Compressed textures for a 4th order model are shown in
Figures 6 and 7. A result using the higher order model
is shown in Figure 8.
bits. To reconstruct the image from
its texture parameters and 1-bit Max quantization, we use an algorithm
similar to Algorithm 2. Instead of synthesizing a
texture from Gaussian noise, we begin with the 1-bit quantized array.
Compressed textures for a 4th order model are shown in
Figures 6 and 7. A result using the higher order model
is shown in Figure 8.
The noise sequence  is generated as follows:
is generated as follows:

where

and the 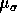 is given in (13).
We estimate the residual as:
is given in (13).
We estimate the residual as:

and  is the sequence which is Max quantized.
is the sequence which is Max quantized.
The image reconstruction from parameters and quantization  is as follows:
is as follows:

where

and  is given in (13);
is given in (13);  is
given in (14).
is
given in (14).
The texture compression algorithm has the same time complexity and
scalability characteristics as Algorithm 4. The image
reconstruction algorithm has the same complexities as
Algorithm 2. Hence these algorithms scale with
image size n and number of processors p.
This algorithm could be used to compress the textures regions in
natural images as part of segmentation based compression schemes
discussed in [27]. Compression factors of 35 have been
obtained for the standard Lena and F-16 images, with no visible
degradations. Compression factors of 80 have been shown to be
feasible when small degradations are permitted in image
reconstruction.



Next: Conclusions
Up: Scalable Data Parallel Algorithms
Previous: Maximum Likelihood Estimate
David A. Bader
dbader@umiacs.umd.edu
 bits. To reconstruct the image from
its texture parameters and 1-bit Max quantization, we use an algorithm
similar to Algorithm 2. Instead of synthesizing a
texture from Gaussian noise, we begin with the 1-bit quantized array.
Compressed textures for a 4th order model are shown in
Figures 6 and 7. A result using the higher order model
is shown in Figure 8.
bits. To reconstruct the image from
its texture parameters and 1-bit Max quantization, we use an algorithm
similar to Algorithm 2. Instead of synthesizing a
texture from Gaussian noise, we begin with the 1-bit quantized array.
Compressed textures for a 4th order model are shown in
Figures 6 and 7. A result using the higher order model
is shown in Figure 8.
 is generated as follows:
is generated as follows:


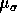 is given in (
is given in (
 is the sequence which is Max quantized.
is the sequence which is Max quantized.
 is as follows:
is as follows:


 is given in (
is given in ( is
given in (
is
given in (