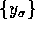We introduce the following approach as an improved method for estimating GMRF parameters of textured images. The method of maximum likelihood gives a better estimate of the texture parameters, since the asymptotic variance of the MLE is lower than that of the LSE. We also show a much faster algorithm for optimizing the joint probability density function which is an extension of the Newton-Raphson method and is also highly parallelizable.
Assuming a toroidal lattice representation for the image
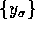and Gaussian structure for noise sequence
, the joint probability density function is the
following:
In (22), 
is the sample correlation estimate at
lag 
. As described in [3] and [6],
the log-likelihood function can be maximized: (Note that 
).
For a square image,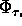 
is given as follows:
This non-linear function F is maximized by using an extension of
the Newton-Raphson method. This new method first generates a
search direction 
by solving the system
Note that this method works well when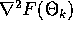 
is a symmetric,
positive-definite Hessian matrix. We then maximize the step in
the search direction, yielding an approximation to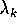 
which
attains the local maximum of 
and
also satisfies the constraints that each of the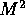 
values in the
logarithm term for F is positive. Finally, an optimality
test is performed. We set 
, and if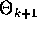 
is sufficiently close to 
,
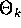the procedure terminates. We give the first and second derivatives of
F with respect to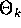 
and 
in
Appendix B.
For a rapid convergence of the Newton-Raphson method, it must be
initialized with a good estimate of parameters close to the global
maximum. We use the least squares estimate given in
Subsection 4.1 as 
, the starting value of the
parameters.
The time complexities per iteration of the MLE algorithm are similar to that of the LSE algorithm analysis given in Subsection 4.1.
In Figures 6 - 8, we show the synthesis using least squares and maximum likelihood estimates for wool weave, wood grain, and tree bark, respectively, obtained from standard textures library. Tables 5, 6, and 7 show the respective parameters for both the LSE and MLE and give their log-likelihood function values. Each example shows that the maximum likelihood estimate improves the parameterization.
In addition, CM-5 timings for these estimates varying machine size, image size, and neighborhood models can be found in Tables 8, 9, 10, and 11, for a 4th order model on this selection of real world textured images, and in Tables 12, 13, 14, and 15, for a higher order model on the same set of images. Similarly, CM-2 timings for these estimates can be found in [2]. Tables 8 - 15 are given in Appendix C.
