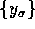The least squares estimate detailed in [6] assumes that
the observations of the GMRF image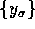 
obey the model
where 
is a zero mean correlated noise sequence with
variance 
and correlation with the following structure:
The conditional distribution is given in (11). Then, for 
, the LSE are:
where 
is the complete set of 
pixels, and toroidal wrap-around is assumed.
For an image of size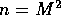 
, step 1.1 has a computational
complexity of O
parallel steps and a
communication complexity of O
. Step 1.2
runs in O
parallel steps.
Step 3 takes O
parallel steps.
Steps 2 and 4 contain a reduction over the entire array, specifically,
finding the sum of the elements in a given parallel variable. As this
is a scan operation, we refer the reader to Subsection 2.4\
for algorithm analysis. Thus, step 2 runs is O
computational parallel steps with O
communications, and steps 4 and 6 run in O
parallel steps with O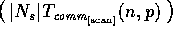
communications. Solving the linear system of equations in step 5 takes
O
computational steps.
The computational complexity of the Least Squares Estimator for an image of size
is
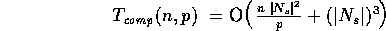
and the communication complexity is
using 
processors.
