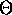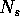The previous section outlined an algorithm for sampling GMRF textured
images using an iterative method. Unfortunately, this algorithm may
have to perform hundreds or even thousands of iterations before a
stable texture is realized. Next we present a scheme which makes use
of two-dimensional Fourier transforms and does not need to iterate.
The Direct GMRF Sampler algorithm is realized from
[6] as follows. We use the following scheme to
reconstruct a texture from its parameters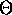 
and a neighborhood
:
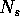where y is the resulting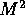 
array of the texture image, and
The sampling process is as follows. We begin with 
, a
Gaussian zero mean noise vector with identity covariance matrix. We
generate its the Fourier series, via the Fast Fourier Transform from
Subsection 2.4, using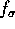 
, the Fourier vector
defined below:
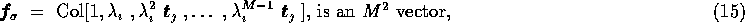
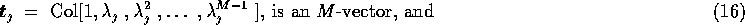
and finally apply (12).
Steps 1, 2, 3, 5.2, 5.3, and 7 all run in O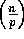
parallel
steps, where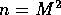 
and p is the number of processors available.
As stated in Subsection 2.4, an n-point FFT, used in
steps 4 and 6, computed on p processors takes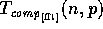 
computation
time and 
communications. Step 5.1 takes O
parallel steps.
The Direct Gaussian MRF Sampler algorithm thus has a computation complexity of
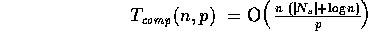
and communication complexity of
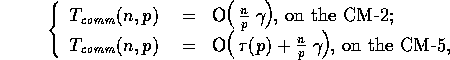
using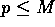 
processors.
Note that the number of gray levels, G, is only used in the last step of the algorithm as a scaling constant. Hence this algorithm scales with image size n and number of processors p, independent of the number of gray levels G used. Notice also that the communication complexity is higher than that of the Gibbs sampler; this is due to the fact that the FFT is a global operation on the image. Our experimental data collected by implementing this algorithm on the CM-2 and the CM-5 confirm our analysis.
