
The parallel algorithm for selection can now be presented, and makes use of the Dynamic Data Redistribution algorithm given in Section 4. The following is run on processor j:
The analysis of the parallel selection algorithm is as follows. For  , in step 1, we solve the problem sequentially in linear time.
For larger n, dynamic data redistribution algorithm is called in
step 2 to ensure that there are
, in step 1, we solve the problem sequentially in linear time.
For larger n, dynamic data redistribution algorithm is called in
step 2 to ensure that there are 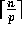 elements
on processors 0 through p-2, and processor p-1 holds the
remaining
elements
on processors 0 through p-2, and processor p-1 holds the
remaining 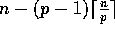 elements. At least
half of the medians found in step 3 are less than or equal to the
splitter. Thus, at least half of the p groups contribute at least
elements. At least
half of the medians found in step 3 are less than or equal to the
splitter. Thus, at least half of the p groups contribute at least
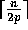 elements that are less than the splitter,
except for the last group and the group containing the splitter
element. Therefore, the total number of elements less than or equal to
the splitter is at least
elements that are less than the splitter,
except for the last group and the group containing the splitter
element. Therefore, the total number of elements less than or equal to
the splitter is at least

Similarly, the number of elements
that are greater than the splitter is at least 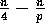 . Thus, in the worst case, the selection algorithm is
called recursively on at most
. Thus, in the worst case, the selection algorithm is
called recursively on at most
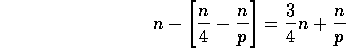
elements.
Using the complexity of the communication primitives as stated in Section 3, it is easy to to derive the recurrence equations for the parallel complexity of our algorithm. Solving these recurrences yields the following complexity:
where m is defined in Eq. (6) to be  , the maximum number of elements initially on any of the
processors. For fixed p, the communication time increases linearly
with m and logarithmically with n, while the computation time
grows linearly with both m and n.
, the maximum number of elements initially on any of the
processors. For fixed p, the communication time increases linearly
with m and logarithmically with n, while the computation time
grows linearly with both m and n.

Figure 6: Performance of Median Algorithm
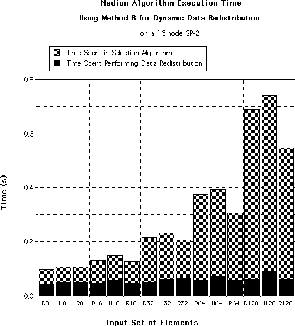
Figure 7: Performance of Median Algorithm on the SP-2
The running time of the median algorithm on the TMC CM-5 using both methods of dynamic data redistribution is given in Figure 6. Similar results are given in Figure 7 for the IBM SP-2. In all data sets, initial data is balanced.