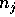 to be
the number of elements initially on processor j, for
to be
the number of elements initially on processor j, for 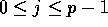 , and hence the total number n of elements is
, and hence the total number n of elements is 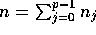 .
.
The selection algorithm makes no initial assumptions about the number
of elements held by each processor, nor the distribution of values on
a single processor or across the p processors. We define 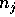 to be
the number of elements initially on processor j, for
to be
the number of elements initially on processor j, for 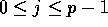 , and hence the total number n of elements is
, and hence the total number n of elements is 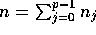 .
.
The input is a shared memory array of elements 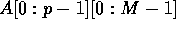 , and
, and
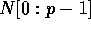 , where
, where 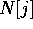 represents
represents 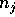 , the number of elements
stored in
, the number of elements
stored in  , and the selection index i. Note that the
median finding algorithm is a special case of the selection problem
where i is equal to
, and the selection index i. Note that the
median finding algorithm is a special case of the selection problem
where i is equal to 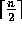 . The output is the
element from A with rank i.
. The output is the
element from A with rank i.
The parallel selection algorithm is motivated by similar sequential
([14], [32]) and parallel ([1],
[25]) algorithms. We use recursion, where at each stage, a
``good'' element from the collection is chosen to split the input into
two partitions, one consisting of all elements less than or equal to
the splitter and the second consisting of the remaining elements.
Suppose there are t elements in the lower partition. If the value of
the selection index i is less than or equal to t, we recurse on
that lower partition with the same index. Otherwise, we recurse on the
higher partition looking for index 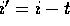 .
.
The choice of a good splitter is as follows. Each processor finds the median of its local elements, and the median of these p medians is chosen.
Since no assumptions are made about the initial distribution of counts or values of elements before calling the parallel selection algorithm, the input data can be heavily skewed among the processors. We use a dynamic redistribution technique which tries to equalize the amount of work assigned to each processor.