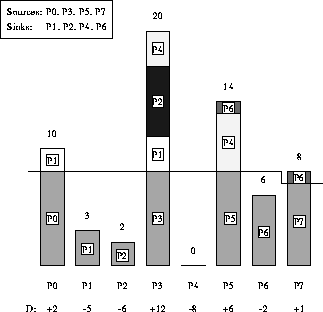
Figure 3: Example of Dynamic Data Redistribution (Method B) with p=8 and n=63

Figure 3: Example of Dynamic Data Redistribution (Method B) with p=8 and n=63
A more efficient dynamic data redistribution algorithm, here referred
to as Method B, makes use of the fact that a processor initially
filled with at least q elements should not need to receive any more
elements, but instead, should send its excess to other processors with
less than q elements. There are pathological cases for which
Method A essentially moves all the data, whereas Method B only
moves a small fraction. For example, if  contains no elements,
and
contains no elements,
and  through
through 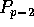 each have q elements, with the remaining
2 q elements held by the last processor, Method A will left
shift all the data by one processor. However, Method B
substantially reduces the communication traffic by taking only the q
extra elements from
each have q elements, with the remaining
2 q elements held by the last processor, Method A will left
shift all the data by one processor. However, Method B
substantially reduces the communication traffic by taking only the q
extra elements from 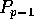 and sending them to
and sending them to 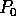 .
.
Dynamic data redistribution Method B calculates the differential
 of the number of elements on processor
of the number of elements on processor  to the balanced
level of q. If
to the balanced
level of q. If  is positive,
is positive,  becomes a source; and
conversely, if
becomes a source; and
conversely, if 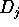 is negative,
is negative,  becomes a sink. The
group of processors labeled as sources will have their excess elements
ranked consecutively, while the processors labeled as sinks similarly
will have their holes ranked. Since the number of elements above the
threshold of q equals the number of holes below the threshold, there
is a one-to-one mapping of data which is used to send data from a
source to the respective holes held by sinks.
becomes a sink. The
group of processors labeled as sources will have their excess elements
ranked consecutively, while the processors labeled as sinks similarly
will have their holes ranked. Since the number of elements above the
threshold of q equals the number of holes below the threshold, there
is a one-to-one mapping of data which is used to send data from a
source to the respective holes held by sinks.
In addition to reduced communication, Method B performs data remapping in-place, without the need for a secondary array of elements used to receive data, as in Method A. Thus, Method B also has reduced memory requirements.
Figure 3 shows the same data redistribution example for
Method B. The heavy line drawn horizontally across the elements
represents the threshold q below which sinks have holes and sources
contain excess elements. Note that 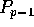 again holds the remainder
of elements when p does not divide the total number of elements
evenly.
again holds the remainder
of elements when p does not divide the total number of elements
evenly.
The SPMD algorithm for Method B is described below. The following is run on processor j:
The analysis for Method B of the parallel dynamic data redistribution algorithm is identical to that of Method A, and is given in Eq. (6). Note that both methods have theoretically similar complexity results, but Method B is superior for the reasons stated earlier.

Figure 4: Dynamic Data Redistribution Algorithms - Method B. The
complexity of our algorithm is essentially linear in 
Figure 4 shows the running time of Method B for
dynamic data redistribution. The top left-hand plate contains results
from the CM-5, the top right-hand from the SP-2. The bottom plate
contains results from the Cray T3D. In the five experiments, on the
32 processors CM-5, the total number of elements n is is 32K. On
the SP-2, the 8 node partition has n = 32K elements, while the
16 node partition has results using both n = 32K and 64K
elements. The T3D experiment also uses 16 nodes and a total number
of elements n = 32K and 64K. Let j represent the processor
label, for 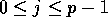 . Then the five input distributions are
defined as
. Then the five input distributions are
defined as
 elements and hence
elements and hence 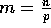 ;
;
 elements and hence
elements and hence  ;
;
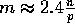 for
for  ;
;
 contains
contains 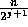 elements, for
elements, for  , and
, and  contains
contains  elements
and hence
elements
and hence 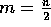 ;
;
The complexity stated in Eq. (6) indicates that the amount of local computation depends only on m (linearly) while the amount of communication increases with both parameters m and p. In particular, for fixed p and a specific machine, we expect the total execution time to increase linearly with m. The results shown in Figure 4 confirm this latter observation.
Note that for the All-on-one input distribution, the dynamic data redistribution results in the same loading as would calling a scatter primitive. In Figure 5 we compare the dynamic data redistribution algorithm performance with that of directly calling a scatter IBM communication primitive on the IBM SP-2, and calling SHMEM primitives on the Cray T3D. In this example, we have used from 2 to 64 wide nodes of the SP-2 and 4 to 128 nodes of the T3D. Note that the performance of our portable redistribution code is close to the low-level vendor supplied communication primitive for the scatter operation. As anticipated by the complexity of our algorithm stated in Eq. (6), the communication overhead increases with p.
Using this dynamic data redistribution algorithm, which we call REDIST, we can now describe the parallel selection algorithm.

Figure 5: Comparison of REDIST vs. Scatter Primitives