


Next: The Block Distributed Memory Model
Up: Practical Parallel Algorithms
Previous: Practical Parallel Algorithms
Consider the problem of finding the median of a set of n elements
that are spread across a p-processor distributed memory machine,
where 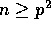 . The median is typically defined as the element
that is the
. The median is typically defined as the element
that is the 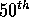 quantile of a set, or the element of rank
quantile of a set, or the element of rank
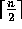 after the data has been sorted in
ascending order. A more general problem is that of selection;
namely, we have to find the element of rank i, for a given parameter
i,
after the data has been sorted in
ascending order. A more general problem is that of selection;
namely, we have to find the element of rank i, for a given parameter
i, 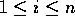 . Parallel sorting trivially solves the selection problem, but
sorting is known to be computationally harder than selection.
. Parallel sorting trivially solves the selection problem, but
sorting is known to be computationally harder than selection.
Previous parallel algorithms for selection ([9],
[23], [31], [25]) and data
redistribution ([28], [34]) tend to be network
dependent or assume the PRAM model, and thus, are not efficient or
portable to current parallel machines. In this paper, we present
algorithms that are shown to be scalable and efficient across a number
of different platforms.
The organization of this paper is as follows.
Section 2 addresses the Block Distributed Memory model
for analyzing shared memory style parallel algorithms. The
Communication Library Primitive operations which are fundamental to
the design of high-level algorithms are introduced in
Section 3. A practical algorithm for the dynamic
redistribution of data derived from these primitives is given in
Section 4. A parallel selection algorithm is described and
analyzed in Section 5, together with experimental results
on a number of platforms.



Next: The Block Distributed Memory Model
Up: Practical Parallel Algorithms
Previous: Practical Parallel Algorithms
David A. Bader
dbader@umiacs.umd.edu
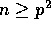 . The median is typically defined as the element
that is the
. The median is typically defined as the element
that is the 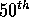 quantile of a set, or the element of rank
quantile of a set, or the element of rank
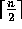 after the data has been sorted in
ascending order. A more general problem is that of selection;
namely, we have to find the element of rank i, for a given parameter
i,
after the data has been sorted in
ascending order. A more general problem is that of selection;
namely, we have to find the element of rank i, for a given parameter
i, 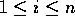 . Parallel sorting trivially solves the selection problem, but
sorting is known to be computationally harder than selection.
. Parallel sorting trivially solves the selection problem, but
sorting is known to be computationally harder than selection.