


Next: Communication Library Primitives
Up: Practical Parallel Algorithms
Previous: Problem Overview
We use the Block Distributed Memory (BDM) Model ([26],
[27]) as a computation model for developing and analyzing
our parallel algorithms on distributed memory machines. This model
allows the design of algorithms using a single address space and does
not assume any particular interconnection topology. The model
captures performance by incorporating a cost measure for
interprocessor communication induced by remote memory accesses. The
cost measure includes parameters reflecting memory latency,
communication bandwidth, and spatial locality. This model allows the
initial placement of data and prefetching.
The complexity of parallel algorithms will be evaluated in terms of
two measures: the computation time 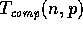 , and the communication time
, and the communication time
 . The measure
. The measure 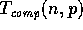 refers to the maximum of the local
computations performed on any processor as measured on the standard
sequential model. The communication time
refers to the maximum of the local
computations performed on any processor as measured on the standard
sequential model. The communication time  refers to the total
amount of communications time spent by the overall algorithm in
accessing remote data. Using the BDM model, an access operation to a
remote location takes
refers to the total
amount of communications time spent by the overall algorithm in
accessing remote data. Using the BDM model, an access operation to a
remote location takes 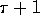 time, and l prefetch read
operations can be executed in
time, and l prefetch read
operations can be executed in 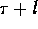 time, where
time, where  is the
normalized maximum latency of any message sent in the communications
network. No processor can send or receive more than one word at a
time.
is the
normalized maximum latency of any message sent in the communications
network. No processor can send or receive more than one word at a
time.
We present several useful communication primitives in [3] and
[4] for the transpose (also known as ``index'' or
``all-to-all personalized'' communication) and the broadcast data
movements. Since these will be important primitives for analyzing our
parallel algorithms, a summary of these communication primitives
follows.



Next: Communication Library Primitives
Up: Practical Parallel Algorithms
Previous: Problem Overview
David A. Bader
dbader@umiacs.umd.edu
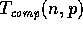 , and the communication time
, and the communication time
 . The measure
. The measure 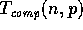 refers to the maximum of the local
computations performed on any processor as measured on the standard
sequential model. The communication time
refers to the maximum of the local
computations performed on any processor as measured on the standard
sequential model. The communication time  refers to the total
amount of communications time spent by the overall algorithm in
accessing remote data. Using the BDM model, an access operation to a
remote location takes
refers to the total
amount of communications time spent by the overall algorithm in
accessing remote data. Using the BDM model, an access operation to a
remote location takes 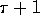 time, and l prefetch read
operations can be executed in
time, and l prefetch read
operations can be executed in 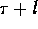 time, where
time, where  is the
normalized maximum latency of any message sent in the communications
network. No processor can send or receive more than one word at a
time.
is the
normalized maximum latency of any message sent in the communications
network. No processor can send or receive more than one word at a
time.