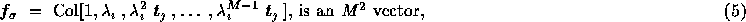In this section, we consider the class of 2-D non-causal models called the Gaussian Markov random field (GMRF) models described in ( [3], [5], and [9]). Pixel grey levels have joint Gaussian distributions and correlations controlled by a number of parameters representing the statistical dependence of a pixel value on the pixel values in a symmetric neighborhood. There are two basic schemes for generating a GMRF image model, both of which are discussed in [3]. The Iterative Gaussian Markov Random Field Sampler is similar to the Gibbs Sampler, but instead of the binomial distribution, we use the continuous Gaussian Distribution as the probability function. An efficient parallel implementation is straightforward and similar to that of the Gibbs Sampler.
The previous section outlined an algorithm for sampling GMRF textured
images using an iterative method. Unfortunately, this algorithm may
have to perform hundreds or even thousands of iterations before a
stable texture is realized. Next we present a scheme which makes use
of two-dimensional Fourier transforms and does not need to iterate.
The Direct GMRF Sampler algorithm is realized from
[3] as follows. We use the following scheme to
reconstruct a texture from its parameters 
and a neighborhood
:
where y is the resulting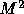 
array of the texture image, and
The sampling process is as follows. We begin with 
, a
Gaussian zero mean noise vector with identity covariance matrix. We
generate its the Fourier series, via the Fast Fourier Transform, using
, the Fourier vector defined below, and finally apply (3).
