A discrete Gibbs random field (GRF) is specified by a probability mass function of the image as follows:
where 
is the energy function, and 
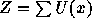, over all
images; G being the number of grey levels, and the image is
of size 
. Except in very special
circumstances, it is not feasible to compute Z. A relaxation-type
algorithm described in [6] simulates a Markov chain through an
iterative procedure that re-adjusts the grey levels at pixel locations
during each iteration. This algorithm sequentially initializes the
value of each pixel using a uniform distribution. Then a single pixel
location is selected at random, and using the conditional distribution
that describes the Markov chain, the new grey level at that location
is selected, dependent only upon the grey levels of the pixels in its
local neighborhood. The sequential algorithm terminates after a given
number of iterations.
The sequential algorithm to generate a Gibbs random field described in
[6] and [7] are used as a basis for our parallel
algorithm. For all the algorithms given in this paper, we
use a symmetric neighborhood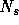 
which is half the size of the
standard neighborhood model N. This implies that if the vector
, then 
, but only
one of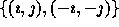 
is in 
.
Each element of array 
is taken to represent the parameter
associated with its corresponding element in 
. We use the
notation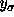 
to represent the grey level of the image at
pixel location 
.
Our Gibbs random field is generated using a simulated annealing type
process. For an image with G grey levels, the probability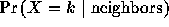 
is binomial with parameter 
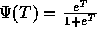, and number of trials G-1. The array
{T} is given in the following equation for a first-order model:
and is a weighted sum of neighboring pixels at each pixel location. Additional examples of {T} for higher order models may be found in [6].
This algorithm is ideal for parallelization. The calculation of {T} requires uniform communications between local processing elements, and all other operations needed in the algorithm are data independent, uniform at each pixel location, scalable, and simple.
An example of a binary synthetic texture generated by the Gibbs Sampler is given in Figure 4.
Table 1 shows the timings of a binary Gibbs sampler for model orders 1, 2, and 4, on the CM-5. More extensive tables for both the CM-2 and CM-5 can be found in [1].
