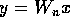 , where
, where 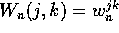 , for
, for
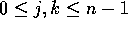 , and
, and 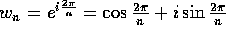 ,
, 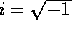 , in
, in
 arithmetic operations.
arithmetic operations.
We next consider the Fast Fourier Transform (FFT) computation. This algorithm
computes the discrete Fourier transform (DFT) of an n-dimensional complex
vector x, defined by 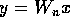 , where
, where 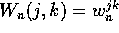 , for
, for
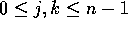 , and
, and 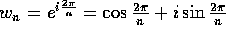 ,
, 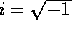 , in
, in
 arithmetic operations.
arithmetic operations.
Our implementation on the BDM model is based on the following well-known
fact (e.g. see [17]). Let the n-dimensional vector x be stored
in the  matrix X in row-major order form, where
p is an arbitrary integer that divides n. Then the DFT of the vector
x is given by
matrix X in row-major order form, where
p is an arbitrary integer that divides n. Then the DFT of the vector
x is given by

where  is the submatrix of
is the submatrix of  consisting of the first
consisting of the first
 rows and the first p columns (twiddle-factor scaling), and
rows and the first p columns (twiddle-factor scaling), and
 is elementwise multiplication. Notice that the resulting output is a
is elementwise multiplication. Notice that the resulting output is a
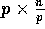 matrix holding the vector
matrix holding the vector 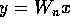 in column major order
form. Equation (1) can be interpreted as computing DFT(
in column major order
form. Equation (1) can be interpreted as computing DFT( )
on each column of X, followed by a twiddle-factor scaling, and finally
computing DFT(p) on each row of the resulting matrix.
)
on each column of X, followed by a twiddle-factor scaling, and finally
computing DFT(p) on each row of the resulting matrix.
Let the BDM machine have p processors such that p divides n and
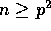 . The initial data layout corresponds to the row major order form
of the data , i.e., the local memory of processor
. The initial data layout corresponds to the row major order form
of the data , i.e., the local memory of processor  will hold
will hold

 . Then the algorithm
suggested by (1) can be performed by the following three stages.
The first stage involves a local computation of a DFT of size
. Then the algorithm
suggested by (1) can be performed by the following three stages.
The first stage involves a local computation of a DFT of size  in each processor, followed by the twiddle-factor scaling (elementwise
multiplication by
in each processor, followed by the twiddle-factor scaling (elementwise
multiplication by  ). The second stage is a communication step
that involves a matrix transposition as outlined in Lemma 3.3.
Finally,
). The second stage is a communication step
that involves a matrix transposition as outlined in Lemma 3.3.
Finally, 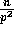 local FFTs each of size p are sufficient to
complete the overall FFT computation on n points. Therefore we have
the following theorem.
local FFTs each of size p are sufficient to
complete the overall FFT computation on n points. Therefore we have
the following theorem.
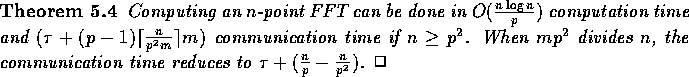
Remark: The algorithm described in [8] can also be implemented on our model
within the same complexity bounds. However our algorithm is somewhat simpler to implement. 