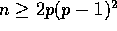 ,
and that the sample sort and the rotate sort are better
when
,
and that the sample sort and the rotate sort are better
when 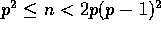 .
.
We first consider the sorting problem on the BDM model.
Three strategies seem to perform best on our model;
these are (1) column sort [15],
(2) sample sort (see e.g. [6] and related references),
and (3) rotate sort [18].
It turns out that the column sort algorithm is best when 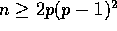 ,
and that the sample sort and the rotate sort are better
when
,
and that the sample sort and the rotate sort are better
when 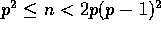 .
.
The column sort algorithm is particularly useful if 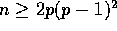 ;
it can be implemented in at most
;
it can be implemented in at most 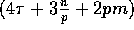 communication time
with
communication time
with  computation time.
When
computation time.
When 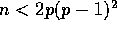 , the column sort algorithm is not practical
since its constant term grows exponentially as n decreases.
The sample sort algorithm is provably efficient when
, the column sort algorithm is not practical
since its constant term grows exponentially as n decreases.
The sample sort algorithm is provably efficient when 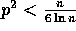 ;
it can be implemented in
;
it can be implemented in
 communication time and
communication time and  computation time with high probability.
computation time with high probability.
The rotate sort algorithm can be implemented in
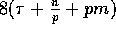 communication time with
communication time with  computation time, whenever
computation time, whenever 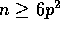 .
.
We begin our description with the column sort algorithm.
Column Sort
The column sort algorithm is a generalization of odd-even mergesort and
can be described as a series of elementary matrix operations.
Let A be an 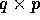 matrix of elements where qp=n, p divides
q, and
matrix of elements where qp=n, p divides
q, and 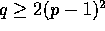 . Initially, each entry of the matrix is one of
the n elements to be sorted. After the completion of the algorithm,
A will be sorted in column major order form. The column sort algorithm
has eight steps. In steps 1, 3, 5, and 7, the elements within each column are
sorted. In steps 2 and 4,
the entries of the matrix are permuted. Each of the permutations is similar to
matrix transposition of Lemma 3.3. Since
. Initially, each entry of the matrix is one of
the n elements to be sorted. After the completion of the algorithm,
A will be sorted in column major order form. The column sort algorithm
has eight steps. In steps 1, 3, 5, and 7, the elements within each column are
sorted. In steps 2 and 4,
the entries of the matrix are permuted. Each of the permutations is similar to
matrix transposition of Lemma 3.3. Since 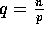 in this case, these
two steps can be done in
in this case, these
two steps can be done in 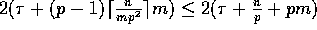 communication time. Each of steps 6 and 8 consists of a
communication time. Each of steps 6 and 8 consists of a  -shift
operation which can be clearly done in
-shift
operation which can be clearly done in 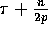 communication time.
Hence the column sort algorithm can be
implemented on our model within
communication time.
Hence the column sort algorithm can be
implemented on our model within 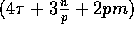 communication
time and
communication
time and 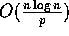 computation time.
Thus, we have the following theorem.
computation time.
Thus, we have the following theorem.

Sample Sort
The second sorting algorithm that we consider in this section is
the sample sort algorithm which is a randomized algorithm
whose running time does not depend on the input distribution of keys but only
depends on the output of a random number generator. We describe
a version of the sample sort algorithm that sorts on the BDM model in at most
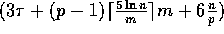 communication time and
communication time and 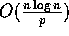 computation time
whenever
computation time
whenever 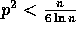 .
The complexity bounds are guaranteed
with high probability if we use the randomized routing algorithm described
in Section 3.
.
The complexity bounds are guaranteed
with high probability if we use the randomized routing algorithm described
in Section 3.
The overall idea of the algorithm has been used in various sample sort algorithms. Our algorithm described below follows more closely the scheme described in [6] for sorting on the connection machine CM-2; however the first three steps are different.
Algorithm Sample_Sort
Input: n elements distributed evenly over a p-processor BDM
such that  .
.
Output: The n elements sorted in column major order.
begin
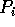 randomly picks a list of
randomly picks a list of 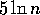 elements from its local memory.
elements from its local memory.
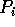 reads all the samples from all the other
processors; hence each processor will have
reads all the samples from all the other
processors; hence each processor will have  samples after
the execution of this step.
samples after
the execution of this step.
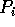 sorts the list of
sorts the list of  samples
and pick
samples
and pick 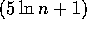 st,
st, 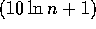 st,
st,  samples as the p-1 pivots.
samples as the p-1 pivots.
 partitions its
partitions its 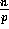 elements
into p sets,
elements
into p sets,  , such that the elements
in set
, such that the elements
in set  belong to the interval between jth pivot and
belong to the interval between jth pivot and 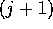 st
pivot, where 0th pivot is
st
pivot, where 0th pivot is  , pth pivot is
, pth pivot is 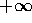 , and
, and
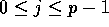 .
.
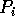 reads all the elements in the p sets,
reads all the elements in the p sets,
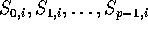 , by using Algorithm Randomized_Routing.
, by using Algorithm Randomized_Routing.
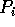 sorts the elements in its
local memory.
sorts the elements in its
local memory.
The following lemma can be immediately deduced from the results of [6].

Next, we show the following theorem.

Proof: Step 2 can be done in  communication time by using a technique similar to that used to prove
Lemma 3.2. By Lemma 5.1, the total number of elements that each processor
reads at Step 5 is at most
communication time by using a technique similar to that used to prove
Lemma 3.2. By Lemma 5.1, the total number of elements that each processor
reads at Step 5 is at most 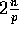 elements with high probability.
Hence, Step 5 can be implemented in
elements with high probability.
Hence, Step 5 can be implemented in 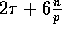 communication time
with high probability using Theorem 3.4.
The computation time for all the steps is clearly
communication time
with high probability using Theorem 3.4.
The computation time for all the steps is clearly 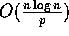 with high probability if
with high probability if  , and the theorem follows.
, and the theorem follows.

Rotate Sort
The rotate sort algorithm [18] sorts elements on a mesh
by alternately applying transformations on the rows and columns.
The algorithm runs in a constant number
of row-transformation and column-transformation phases (16 phases).
We assume here that 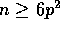 .
.
Naive implementation of the original algorithm on our model requires 14 simple
permutations similar to matrix transpositions, and 14 local sortings
within each processor.
We slightly modify the algorithm so that the algorithm can be implemented
on our model with
8 simple permutations and at most 14 local sortings within each processor.
Since each such simple permutation can be performed on our model
in 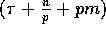 communication time,
this algorithm can be implemented in
communication time,
this algorithm can be implemented in
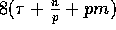 communication time
and
communication time
and 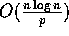 computation time on the BDM model.
computation time on the BDM model.
For simplicity, we assume that 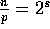 and
and 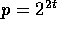 , where
, where
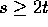 . The results can be generalized to other values of n and p.
A slice is a subarray of size
. The results can be generalized to other values of n and p.
A slice is a subarray of size 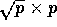 ,
consisting of all rows i such that
,
consisting of all rows i such that 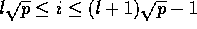 for some
for some  . A block
is a subarray of size
. A block
is a subarray of size 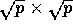 , consisting of all positions
, consisting of all positions
 such that
such that 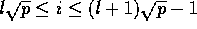 and
and
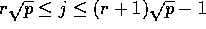 for some
for some  and
and 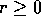 .
.
We now describe the algorithm briefly; all the details appear in [18]. We begin by specifying three procedures, which serve as building blocks for the main algorithm. Each procedure consists of a sequence of phases that accomplish a specific transformation on the array.
Procedure BALANCE: Input array is of size  .
.
(a) Sort all the columns downwards.
(b) Rotate each row i  positions to the right.
positions to the right.
(c) Sort all the columns downwards.
Procedure UNBLOCK:
(a) Rotate each row i  positions to the
right.
positions to the
right.
(b) Sort all the columns downwards.
Procedure SHEAR:
(a) Sort all even-numbered columns downwards and all the odd-numbered
columns upwards.
(b) Sort all the rows to the right.
The overall sorting algorithm is the following.
Algorithm ROTATESORT
1. BALANCE the input array of size 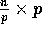 .
.
2. Sort all the rows to the right.
3. UNBLOCK the array.
4. BALANCE each slice as if it were a  array lying on its
side.
array lying on its
side.
5. UNBLOCK the array.
6. ``Transpose'' the array.
7. SHEAR the array.
8. Sort all the columns downwards.
For the complete correctness proof of the algorithm, see [18].
We can easily prove that this algorithm can be performed in at most
14 local sorting steps within each processor. We can also prove that
each of the simple permutations can be done in
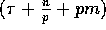 communication time in a similar way
as in Lemma 3.3. Steps 1, 3, 5, and 6
can each be done with one simple permutation. Steps 2 and 4 also
can each be done with one simple permutation by overlapping their
second permutations with the first permutations of steps 3 and 5 respectively.
Originally, Step 7 is ``Repeat SHEAR three times'' which is designed
for removing six ``dirty rows'' that are left after Step 5;
hence, this step requires 6 simple permutations
on our model. Since we assumed
communication time in a similar way
as in Lemma 3.3. Steps 1, 3, 5, and 6
can each be done with one simple permutation. Steps 2 and 4 also
can each be done with one simple permutation by overlapping their
second permutations with the first permutations of steps 3 and 5 respectively.
Originally, Step 7 is ``Repeat SHEAR three times'' which is designed
for removing six ``dirty rows'' that are left after Step 5;
hence, this step requires 6 simple permutations
on our model. Since we assumed 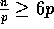 , the length of each column
is larger than that of each row, and we can reduce the number of the
applications of SHEAR procedure in Step 7 by transposing the matrix in Step 6.
Thus, since the assumption
, the length of each column
is larger than that of each row, and we can reduce the number of the
applications of SHEAR procedure in Step 7 by transposing the matrix in Step 6.
Thus, since the assumption 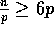 implies that there are
at most two dirty columns after the execution of Step 6,
one application of procedure SHEAR is enough in Step 7 for removing
the two dirty columns and we have the following theorem.
implies that there are
at most two dirty columns after the execution of Step 6,
one application of procedure SHEAR is enough in Step 7 for removing
the two dirty columns and we have the following theorem.
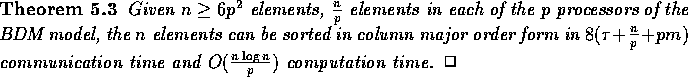
Notice that if 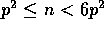 , we need to repeat SHEAR
, we need to repeat SHEAR
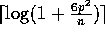 times at Step 7 for removing the
dirty columns, and the communication time for
Algorithm ROTATESORT is at most
times at Step 7 for removing the
dirty columns, and the communication time for
Algorithm ROTATESORT is at most 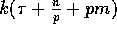 , where
, where
 .
.
Other Sorting Algorithms
When the given elements are integers between 0 and 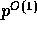 , the local sorting
needed in each of the previous algorithms can be done in
, the local sorting
needed in each of the previous algorithms can be done in 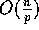 computation time by applying radix sort.
Hence we have the following corollary.
computation time by applying radix sort.
Hence we have the following corollary.

Two other sorting algorithms are worth considering:
(1) radix sort (see e.g. [6] and
related references) and (2) approximate median sort [2,22].
The radix sort can be performed on our model in
 computation
time and
computation
time and  communication time,
where b is the number of bits in the representation of the keys, r
is such that the algorithm examines the keys to be sorted r-bits at a time,
and
communication time,
where b is the number of bits in the representation of the keys, r
is such that the algorithm examines the keys to be sorted r-bits at a time,
and 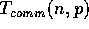 is the communication time for routing a general permutation
on n elements (and hence the bounds in the above corollary apply).
The approximate median sort, which is similar to
sample sort with no randomization used but with p-1 elements
picked from each processor after sorting the elements in each processor,
can be done on our model in
is the communication time for routing a general permutation
on n elements (and hence the bounds in the above corollary apply).
The approximate median sort, which is similar to
sample sort with no randomization used but with p-1 elements
picked from each processor after sorting the elements in each processor,
can be done on our model in
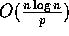 computation time and in at most
computation time and in at most
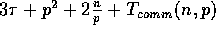 communication time,
if
communication time,
if 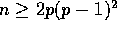 .
.