


Next: References
Up: SortingFFT, and
Previous: Fast Fourier Transform
We finally consider the problem of multiplying two  matrices A and
B. We assume that
matrices A and
B. We assume that 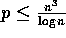 .
We partition each of the matrices A and B
into
.
We partition each of the matrices A and B
into 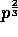 submatrices, say
submatrices, say
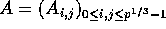 and
and
 , where
each of
, where
each of 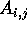 and
and  is of size
is of size
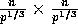 assuming without loss of
generality that
assuming without loss of
generality that 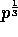 is an integer that divides n.
For simplicity we view the processors indices are arranged as a cube
of size
is an integer that divides n.
For simplicity we view the processors indices are arranged as a cube
of size  ,
that is, they are given by
,
that is, they are given by 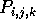 , where
, where
 . We show that product C=AB can be
computed in
. We show that product C=AB can be
computed in 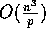 computation time
and
computation time
and 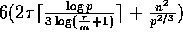 communication time. The overall strategy is similar to the one used in
[1,10], where some related experimental results supporting
the efficiency of the algorithm appear in [10].
Before presenting the algorithm, we establish the following lemma.
communication time. The overall strategy is similar to the one used in
[1,10], where some related experimental results supporting
the efficiency of the algorithm appear in [10].
Before presenting the algorithm, we establish the following lemma.
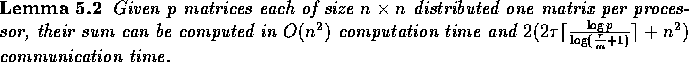
Proof: We partition the
p processors into  groups such that each group contains k processors, where
groups such that each group contains k processors, where
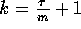 . Using the matrix transposition algorithm, we put the first set of
. Using the matrix transposition algorithm, we put the first set of
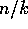 rows of each matrix in a group into the first processor of that group, the second
set of
rows of each matrix in a group into the first processor of that group, the second
set of 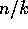 rows into the second processor, and so on. Then for each processor, we
add the k submatrices
locally. At this point, each of the processors in a group holds an
rows into the second processor, and so on. Then for each processor, we
add the k submatrices
locally. At this point, each of the processors in a group holds an 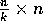 portion of
the sum matrix corresponding to the initial matrices stored in
these processors. We continue with the same strategy by adding each set of
k submatrices within a group of k processors. However this time the submatrices
are partitioned along the columns resulting in submatrices of size
portion of
the sum matrix corresponding to the initial matrices stored in
these processors. We continue with the same strategy by adding each set of
k submatrices within a group of k processors. However this time the submatrices
are partitioned along the columns resulting in submatrices of size  .
We repeat the procedure
.
We repeat the procedure  times at which time
each processor has an
times at which time
each processor has an  portion of the overall
sum matrix. We then collect all the submatrices into a single processor.
The complexity bounds follow as in the proof of Theorem 3.3.
portion of the overall
sum matrix. We then collect all the submatrices into a single processor.
The complexity bounds follow as in the proof of Theorem 3.3.

Algorithm Matrix_Multiplication
Input: Two 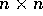 matrices A and B such that
matrices A and B such that
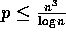 .
Initially, submatrices
.
Initially, submatrices  and
and 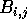 are stored in processor
are stored in processor
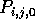 , for each
, for each 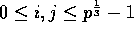 .
.
Output: Processor  holds the submatrix
holds the submatrix  , where
, where
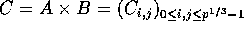 , and each
, and each 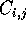 is of size
is of size 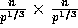 .
.
begin
- [Step 1]
- Processor
 reads blocks
reads blocks 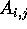 and
and 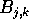 that are initially stored in processors
that are initially stored in processors  and
and 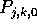 respectively. Each
such block will be read concurrently by
respectively. Each
such block will be read concurrently by 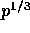 processors.
This step can be performed in
processors.
This step can be performed in
 communication time by using the first algorithm described in Theorem 3.3.
communication time by using the first algorithm described in Theorem 3.3.
- [Step 2]
- Each processor multiplies the two submatrices stored
in its local memory. This step can be done in
 computation time.
computation time.
- [Step 3]
- For each
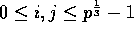 , the sum of
the product submatrices in the
, the sum of
the product submatrices in the 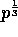 processors
processors  ,
for
,
for 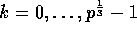 , is computed and stored in processor
, is computed and stored in processor
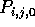 .
This step can be done in
.
This step can be done in  computation time and in
computation time and in
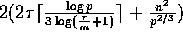 communication time using the algorithm described in Lemma 5.2.
communication time using the algorithm described in Lemma 5.2.
end
Therefore we have the following theorem.

Remark: We could have used the second algorithm described in Theorem 3.3 to
execute Steps 1 and 3 of the matrix multiplication algorithm. The resulting communication
bound would be at most  .
. 



Next: References
Up: SortingFFT, and
Previous: Fast Fourier Transform
joseph@umiacs.umd.edu
 matrices A and
B. We assume that
matrices A and
B. We assume that 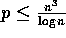 .
We partition each of the matrices A and B
into
.
We partition each of the matrices A and B
into 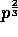 submatrices, say
submatrices, say
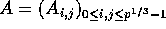 and
and
 , where
each of
, where
each of 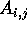 and
and  is of size
is of size
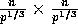 assuming without loss of
generality that
assuming without loss of
generality that 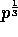 is an integer that divides n.
For simplicity we view the processors indices are arranged as a cube
of size
is an integer that divides n.
For simplicity we view the processors indices are arranged as a cube
of size  ,
that is, they are given by
,
that is, they are given by 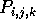 , where
, where
 . We show that product C=AB can be
computed in
. We show that product C=AB can be
computed in 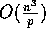 computation time
and
computation time
and 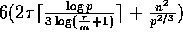 communication time. The overall strategy is similar to the one used in
[1,10], where some related experimental results supporting
the efficiency of the algorithm appear in [10].
Before presenting the algorithm, we establish the following lemma.
communication time. The overall strategy is similar to the one used in
[1,10], where some related experimental results supporting
the efficiency of the algorithm appear in [10].
Before presenting the algorithm, we establish the following lemma.
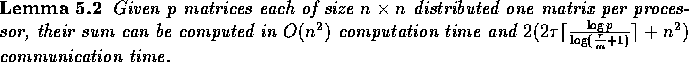
 groups such that each group contains k processors, where
groups such that each group contains k processors, where
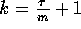 . Using the matrix transposition algorithm, we put the first set of
. Using the matrix transposition algorithm, we put the first set of
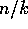 rows of each matrix in a group into the first processor of that group, the second
set of
rows of each matrix in a group into the first processor of that group, the second
set of 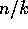 rows into the second processor, and so on. Then for each processor, we
add the k submatrices
locally. At this point, each of the processors in a group holds an
rows into the second processor, and so on. Then for each processor, we
add the k submatrices
locally. At this point, each of the processors in a group holds an 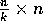 portion of
the sum matrix corresponding to the initial matrices stored in
these processors. We continue with the same strategy by adding each set of
k submatrices within a group of k processors. However this time the submatrices
are partitioned along the columns resulting in submatrices of size
portion of
the sum matrix corresponding to the initial matrices stored in
these processors. We continue with the same strategy by adding each set of
k submatrices within a group of k processors. However this time the submatrices
are partitioned along the columns resulting in submatrices of size  .
We repeat the procedure
.
We repeat the procedure  times at which time
each processor has an
times at which time
each processor has an  portion of the overall
sum matrix. We then collect all the submatrices into a single processor.
The complexity bounds follow as in the proof of Theorem 3.3.
portion of the overall
sum matrix. We then collect all the submatrices into a single processor.
The complexity bounds follow as in the proof of Theorem 3.3.

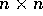 matrices A and B such that
matrices A and B such that
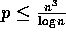 .
Initially, submatrices
.
Initially, submatrices  and
and 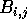 are stored in processor
are stored in processor
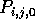 , for each
, for each 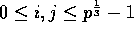 .
. holds the submatrix
holds the submatrix  , where
, where
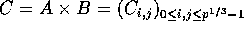 , and each
, and each 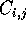 is of size
is of size 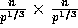 .
.
 reads blocks
reads blocks 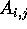 and
and 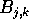 that are initially stored in processors
that are initially stored in processors  and
and 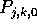 respectively. Each
such block will be read concurrently by
respectively. Each
such block will be read concurrently by 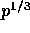 processors.
This step can be performed in
processors.
This step can be performed in
 communication time by using the first algorithm described in Theorem 3.3.
communication time by using the first algorithm described in Theorem 3.3.
 computation time.
computation time.
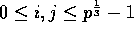 , the sum of
the product submatrices in the
, the sum of
the product submatrices in the 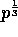 processors
processors  ,
for
,
for 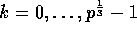 , is computed and stored in processor
, is computed and stored in processor
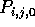 .
This step can be done in
.
This step can be done in  computation time and in
computation time and in
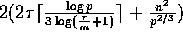 communication time using the algorithm described in Lemma 5.2.
communication time using the algorithm described in Lemma 5.2.

 .
. 