


Next: Communication Primitive: REDUCE
Up: Communication Library Primitives
Previous: Communication Primitive: BCAST
Given an associative operator 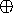 (e.g. +,
(e.g. +, 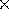 ,
,  ,
,
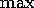 , etc.) and a shared input array
, etc.) and a shared input array 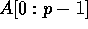 on a p processor
partition, distributed with one element per processor, the
PREFIX Communication Library Primitive coalesces the data such that
each processor k contains a single element
on a p processor
partition, distributed with one element per processor, the
PREFIX Communication Library Primitive coalesces the data such that
each processor k contains a single element 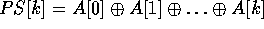 . Parallel computers can handle this
efficiently when the element
. Parallel computers can handle this
efficiently when the element  is assumed to reside on processor
k [10], and SPLIT-C implements this as a primitive
library function. An analysis for this operation on the BDM model is
given in [4]. Since these rounds can be realized with an
CONCAT primitive operation followed by O
is assumed to reside on processor
k [10], and SPLIT-C implements this as a primitive
library function. An analysis for this operation on the BDM model is
given in [4]. Since these rounds can be realized with an
CONCAT primitive operation followed by O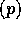 local
computation of the prefix-sums, the resulting complexity is
local
computation of the prefix-sums, the resulting complexity is

Note that our algorithm can perform a stronger operation for the same
complexity; namely, all p prefix-sums values can be made available
as local elements on all processors. Thus, each processor k contains
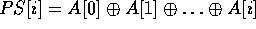 , for all
, for all 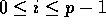 . This is equivalent to calling
CONCAT
. This is equivalent to calling
CONCAT PREFIX
PREFIX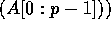 .
.



Next: Communication Primitive: REDUCE
Up: Communication Library Primitives
Previous: Communication Primitive: BCAST
David A. Bader
dbader@umiacs.umd.edu
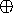 (e.g. +,
(e.g. +, 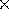 ,
,  ,
,
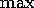 , etc.) and a shared input array
, etc.) and a shared input array 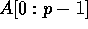 on a p processor
partition, distributed with one element per processor, the
PREFIX Communication Library Primitive coalesces the data such that
each processor k contains a single element
on a p processor
partition, distributed with one element per processor, the
PREFIX Communication Library Primitive coalesces the data such that
each processor k contains a single element 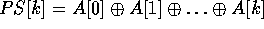 . Parallel computers can handle this
efficiently when the element
. Parallel computers can handle this
efficiently when the element  is assumed to reside on processor
k [10], and SPLIT-C implements this as a primitive
library function. An analysis for this operation on the BDM model is
given in [4]. Since these rounds can be realized with an
CONCAT primitive operation followed by O
is assumed to reside on processor
k [10], and SPLIT-C implements this as a primitive
library function. An analysis for this operation on the BDM model is
given in [4]. Since these rounds can be realized with an
CONCAT primitive operation followed by O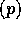 local
computation of the prefix-sums, the resulting complexity is
local
computation of the prefix-sums, the resulting complexity is

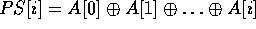 , for all
, for all 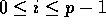 . This is equivalent to calling
CONCAT
. This is equivalent to calling
CONCAT PREFIX
PREFIX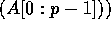 .
.