Another useful data movement primitive is BCAST broadcasting
primitive. An efficient BDM algorithm is given ([3],
[26]) which takes q elements 
on a single
processor and broadcasts them to the other p-1 processors using just
two TRANSPOSE Communication Primitives.
An efficient algorithm for broadcasting no greater than p elements
from one processor (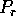
) to the remaining p-1 processors is to
perform the CONCAT communication primitive, such that processors
only prefetch data when it is from processor r. This algorithm is
identical in complexity to Eq. (2). On the other
hand, this problem can be solved using k-ary balanced tree algorithm
[26], in which case the communication would be 
.
For larger q, a more efficient algorithm to broadcast the q
elements from a single processor to p processors is based on the
TRANSPOSE primitive. Processor r holds the q elements to be
broadcast in the first column of matrix A. We perform the
TRANSPOSE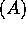
primitive, thus, giving every processor 
elements. Each processor then locally rearranges the data so that an
additional TRANSPOSE data movement will result in each processor
holding a copy of all the q elements in its column of A
[26].
The analysis of this BCAST algorithm is simple. Since this algorithm just performs two TRANSPOSE Communication Primitives, the complexities of the BCAST Primitive are
See [3] and [4] for algorithmic details, performance analysis, and empirical results for these communication primitives.
