


Next: Complexity of Some
Up: Parallel Algorithm Analysis
Previous: Simple and Regular
The CM-2 contains from 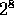 to
to  Sprint nodes interconnected
by a binary hypercube network. Each Sprint node consists of two chips
of processors, each with 16 bit-serial processing elements. Thus, the
CM-2 has configurations ranging between 8K and 64K, inclusive,
bit-serial processors. In this analysis, we view each Sprint node as a
single 32-bit processing node.
Sprint nodes interconnected
by a binary hypercube network. Each Sprint node consists of two chips
of processors, each with 16 bit-serial processing elements. Thus, the
CM-2 has configurations ranging between 8K and 64K, inclusive,
bit-serial processors. In this analysis, we view each Sprint node as a
single 32-bit processing node.
The CM-2 programming model of 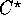 uses a canonical data layout
similar to that on the CM-5 described in Section 2.2.1\
([39], [38], [44], [4]).
The only difference on the CM-2 and CM-5 is that the Sprint node, or
major grid, portion of each data element address is in reflected
binary gray code, insuring that nearest neighbor communications are at
most one hop away in the hypercube interconnection network.
uses a canonical data layout
similar to that on the CM-5 described in Section 2.2.1\
([39], [38], [44], [4]).
The only difference on the CM-2 and CM-5 is that the Sprint node, or
major grid, portion of each data element address is in reflected
binary gray code, insuring that nearest neighbor communications are at
most one hop away in the hypercube interconnection network.
We now analyze the complexity for a regular grid shift on the CM-2.
Each node holds a contiguous subgrid of  data elements.
During a grid shift, O
data elements.
During a grid shift, O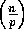 elements remain local to each
Sprint node, giving
elements remain local to each
Sprint node, giving

Each Sprint node will send border elements to their destination node.
By the canonical layout, we are assured that this destination is an
adjacent node in the hypercube. Every Sprint node will send and
receive elements along unique paths of the network. In this model, we
neglect  since we are using direct hardware links which do
not incur the overhead associated with packet routing analyses. Thus,
each Sprint node will need to send and receive
O
since we are using direct hardware links which do
not incur the overhead associated with packet routing analyses. Thus,
each Sprint node will need to send and receive
O elements, yielding a communications
complexity of
elements, yielding a communications
complexity of

where 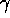 is the CM-2 transmission rate into the network.
is the CM-2 transmission rate into the network.
Therefore, on a CM-2 with p Sprint nodes, a regular grid shift
of a 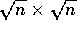 data array has the following time
complexity analyses:
data array has the following time
complexity analyses:

As shown, a regular grid shift on the CM-2 is scalable for the array
size and the machine size.



Next: Complexity of Some
Up: Parallel Algorithm Analysis
Previous: Simple and Regular
David A. Bader
dbader@umiacs.umd.edu
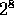 to
to  Sprint nodes interconnected
by a binary hypercube network. Each Sprint node consists of two chips
of processors, each with 16 bit-serial processing elements. Thus, the
CM-2 has configurations ranging between 8K and 64K, inclusive,
bit-serial processors. In this analysis, we view each Sprint node as a
single 32-bit processing node.
Sprint nodes interconnected
by a binary hypercube network. Each Sprint node consists of two chips
of processors, each with 16 bit-serial processing elements. Thus, the
CM-2 has configurations ranging between 8K and 64K, inclusive,
bit-serial processors. In this analysis, we view each Sprint node as a
single 32-bit processing node.
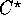 uses a canonical data layout
similar to that on the CM-5 described in Section
uses a canonical data layout
similar to that on the CM-5 described in Section  data elements.
During a grid shift, O
data elements.
During a grid shift, O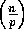 elements remain local to each
Sprint node, giving
elements remain local to each
Sprint node, giving

 since we are using direct hardware links which do
not incur the overhead associated with packet routing analyses. Thus,
each Sprint node will need to send and receive
O
since we are using direct hardware links which do
not incur the overhead associated with packet routing analyses. Thus,
each Sprint node will need to send and receive
O elements, yielding a communications
complexity of
elements, yielding a communications
complexity of

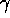 is the CM-2 transmission rate into the network.
is the CM-2 transmission rate into the network.
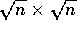 data array has the following time
complexity analyses:
data array has the following time
complexity analyses:
