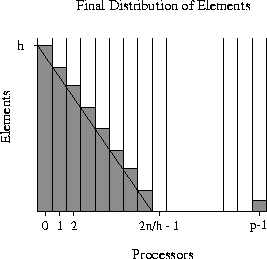
Figure 1: Final distribution of the keys corresponding to our input data sets
We examine the performance of our h-relation algorithm on various
configurations of the IBM SP-2 and Cray T3D, using four values of h:
, 
, 
, and 
.
More results are given in [4]. The data sets used in these
experiments are defined as follows. Our input of size n is initially
distributed cyclically across the p processors such that each
processor 
initially holds 
keys, for 
. For the input consists of 
keys labelled for 
, followed by 
keys labelled for 
, and so forth, (with 
keys
labelled for ), with the last 
keys
labelled for 
. Note that this results in the same data
movement as the transpose primitive
. For 
, instead
of an equal number of elements destined for each processor, the
function 
, for ( 
), is characterized by
The result of this data movement, shown in Figure 1,
is that processor 0 receives the largest imbalance of elements, i.e.
h, while other processors receive varying block sizes ranging from
0 to at most h. For 
, approximately
processors receive no elements, and hence this
represents an extremely unbalanced case.
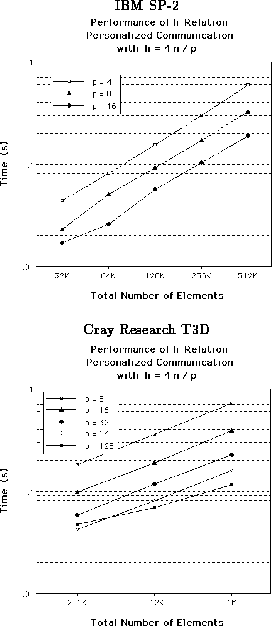
Figure 2: Performance of personalized communication ( 
) with respect to machine and problem size.
As shown in Figure 2, the time to route an
h-relation personalized communication for a given input size on a
varying number of processors (p) scales inversely with p whenever
n is large compared with p. However, for inputs which are small compared
with the machine size, the communication time is dominated by
O 
as shown in the case of the 128-processor Cray T3D with
n = 256K.
