 arithmetic operations per iteration for an image of size
arithmetic operations per iteration for an image of size 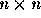 with G grey levels. The implementations known to the authors are
slow and operate on images of size
with G grey levels. The implementations known to the authors are
slow and operate on images of size 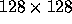 or smaller.
or smaller.
Random Fields have been successfully used to sample and synthesize
textured images (e.g. [6], [4],
[9], [7], [5]).
Texture analysis has applications in image segmentation and
classification, biomedical image analysis, and automatic detection of
surface defects. Of particular interest are the models that specify
the statistical dependence of the grey level at a pixel on those of
its neighborhood. There are several well-known algorithms describing
the sampling process for generating synthetic textured images, and
algorithms that yield an estimate of the parameters of the assumed
random process given a textured image. Impressive results related to
real-world imagery have appeared in the literature ([6],
[7], [5], [8], [3]).
However, all these algorithms are quite computationally demanding
because they typically require on the order of  arithmetic operations per iteration for an image of size
arithmetic operations per iteration for an image of size 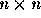 with G grey levels. The implementations known to the authors are
slow and operate on images of size
with G grey levels. The implementations known to the authors are
slow and operate on images of size 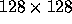 or smaller.
or smaller.
In this paper, we develop scalable data parallel algorithms for implementing the most important texture sampling and synthesis algorithms. The data parallel model is an architecture-independent programming model that allows an arbitrary number of virtual processors to operate on large amounts of data in parallel. All the algorithms described in this paper have been implemented and thoroughly tested on a Connection Machine CM-2 and a Connection Machine CM-5.
Section 2 develops parallel algorithms for texture synthesis using Gibbs and Gaussian Markov Random Fields. Parameter estimation for Gaussian Markov Random Field textures, using least squares, as well as maximum likelihood techniques, are given in Section 3. Conclusions are given in Section 4.