Consider the problem of sorting n elements equally distributed
amongst p processors, where we assume without loss of generality that p
divides n evenly. The idea behind sorting by regular sampling
is to find a set of
p - 1 splitters to partition the n input elements
into p groups indexed from 1 up to p such that every element
in the 
group is less than or equal to each of the elements in
the 
group, for 
. Then the task of
sorting each of the p groups
can be turned over to the correspondingly indexed processor, after which
the n elements will be arranged in sorted order. The
efficiency of this algorithm obviously depends on how well we divide the
input, and this in turn depends on how evenly we choose the splitters.
One way to choose the splitters is by regularly sampling the sorted
input elements at each processor - hence the name Sorting by
Regular Sampling.
A previous version of regular sample
sort [18, 16], known as Parallel Sorting by Regular Sampling
(PSRS) , first sorts the 
elements at each processor and
then selects every 
element as a
sample. These samples are then routed to a single processor,
where they are sorted and every 
sample is selected as a
splitter. Each processor then uses these splitters to
partition the sorted input values and then routes the resulting
subsequences to the appropriate destinations, after which local
merging of these subsequences is done to complete the sorting process.
The first difficulty
with this approach is the load balance. There exist inputs for which
at least one processor will be left with
as many as 
elements
at the completion of sorting.
This could be reduced by choosing more samples, but this would also
increase the overhead. And no matter how many samples are chosen,
previous studies have shown that the load balance would still deteriorate
linearly with the number of duplicates [16]. One could, of course,
tag each item with a unique value, but this would also double the cost of
both memory access and interprocessor communication. The other
difficulty is that no matter how the routing is scheduled, there exist
inputs that give rise to large variations in the number of elements
destined for different processors, and this in turn results in an
inefficient use of the communication bandwidth. Moreover, such an
irregular communication scheme cannot take advantage of the regular
communication primitives proposed under the MPI standard [17].
In our algorithm, which is parameterized by a sampling ratio
s 
, we guarantee that, at the
completion of sorting, each processor will have at most 
elements, while incurring no overhead in
gathering the set of samples used to identify the splitters.
This bound
holds regardless of the number of duplicate elements present in the input.
Moreover, we are able to replace the irregular routing with exactly two
calls to our transpose primitive.
The pseudocode for our algorithm is as follows:
sorts each of its input values using an appropriate
sequential sorting algorithm. For integers we use the radix sort
algorithm, whereas for floating point numbers we use the merge sort
algorithm. The sorted data is then ``dealt'' into p bins so that the
item in the sorted order is placed into the
position of the 
bin. routes the contents of bin
j to processor 
, for 
, which is
equivalent to performing a transpose operation with block size
.
selects each 
element as a sample, for 
and a given value of s . merges the p sorted
subsequences of samples and then selects each 
sample as 
, for 
. By default,
the splitter is the largest value allowed by the data type used.
Additionally, binary search is used to compute for the set of samples
with indices (ks-s+1) through (ks) the number of samples
which share the same value as . broadcasts the Splitter
and Est arrays to the other p - 1 processors. uses binary search to
define for each of the p sorted sequences received
in Step (2) and each of the p splitters a subsequence 
.
The set of p subsequences 
associated with 
all contain values
which are greater than or equal to 
and
less then or equal to , and collectively include
at most 
elements with the same
value as . routes the p
subsequences associated with
to processor , for . Since no two
processors will exchange more than 
elements, this is equivalent to
performing a transpose operation with block size
. ``unshuffles'' all
those subsequences sharing a common origin in Step (2). merges the p
consolidated subsequences to produce the
column of the sorted array.
Before establishing the complexity of this algorithm, we need to establish the following theorem.
Theorem 1: The number of elements sent by processor
to processor in Step (7) is at most
for i = p and
for i < p.
Consequently, at the completion of the algorithm, no processor holds
more than elements,
for 
and .
Proof:
Let 
be the set of samples from the sorted array of samples
in Step (4) with indices (js - s + 1) through (js), inclusively.
Let 
be the subset of samples in originating from
processor , and let 
be the cardinality of .
Let 
, let 
be the number of samples
in with value less than 
, and let
be the number of samples in
with value . Let
,
let 
be the cardinality of
, let 
be the number of samples
in with value less than , and let
be the number of samples in
with value . Obviously, 
will only be
nonzero if 
. Finally, for simplicity of
discussion but without loss of generality,
we assume that n is a constant multiple of 
.
Clearly, each sample can be mapped in a one-to-one fashion to the sorted
input generated during Step (1) (but before being distributed amongst
the bins). For example, the first sample in
maps to the 
element in the
sorted input at processor , the second sample in
maps to the 
element in the
sorted input at processor , and so forth up to the 
element which maps to the 
element in the sorted input at processor . Hence, it follows that
elements in the sorted input
of Step (1) at processor will be less than ,
where 
.
It is also true that at least 
elements in the sorted input of
Step (1) will be less than or equal to , where
.
The shuffling of Step (1) together with the transpose of
Step (2) maps the 
element at processor into
the 
position of the
subarray at processor 
, a subarray which we
will denote as 
. Now,
elements in 
will be less than and
will unequivocally route to processors 
through ,
where:
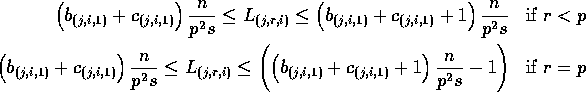
Furthermore, at least 
elements in
will be less than or equal to , where
. This means
that the p subarrays at processor 
collectively have at least
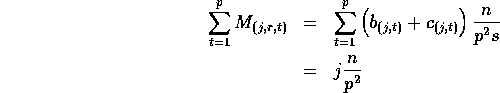
elements which are greater than or equal to . Furthermore,
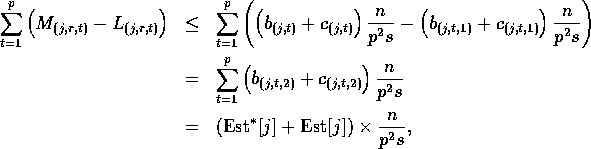
where is the number of elements
equal to which the algorithm in Step (6) will seek
to route to processor and
is the number of elements
equal to which the algorithm in Step (6) will seek
to route to processors through 
.
From this it follows that the algorithm will always be able to route
a minimum of 
elements to processors through .
On the other hand, the maximum number of elements that will be routed by
this algorithm to these processors is:
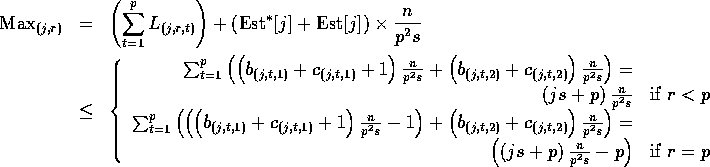
Hence, the maximum number of elements send by processor to
processor is:
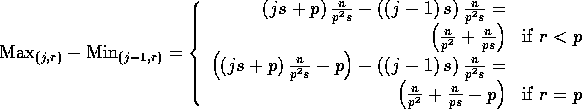
and Theorem 1 follows.
With the results of Theorem 1, the analysis of our algorithm
for sorting by regular sampling is as follows. Steps (3), (4),
(6), (8), and (9) require O(sp), 
,
, 
, and
time,
respectively.
The cost of sequential sorting in Step (1) depends on the data type -
sorting integers using radix sort requires 
time, whereas
sorting floating point numbers using merge sort requires
time.
Steps (2), (5), and
(7) call the communication primitives transpose,
bcast, and transpose, respectively. The analysis of these
primitives in [6] shows that these three steps require
,
, and
,
respectively. Hence, with high probability, the overall complexity of our
sorting algorithm is given (for floating point numbers) by
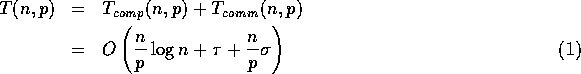
for and .
Clearly, our algorithm is asymptotically optimal with very small coefficients. But a theoretical comparison of our running time with previous sorting algorithms is difficult, since there is no consensus on how to model the cost of the irregular communication used by the most efficient algorithms. Hence, it is very important to perform an empirical evaluation of an algorithm using a wide variety of benchmarks, as we will do next.