A New Sample Sort Algorithm

Consider the problem of sorting n elements equally distributed amongst p processors, where we assume without loss of generality that p divides n evenly. The idea behind sample sort is to find a set of p - 1 splitters to partition the n input elements into p groups indexed from 1 up to p such that every element in the group is less than or equal to each of the elements in the group, for . Then the task of sorting each of the p groups can be turned over to the correspondingly indexed processor, after which the n elements will be arranged in sorted order. The efficiency of this algorithm obviously depends on how evenly we divide the input, and this in turn depends on how well we choose the splitters. One way to choose the splitters is by randomly sampling the input elements at each processor - hence the name sample sort.

Previous versions of sample sort [21, 10, 17, 15] have randomly chosen s samples from the elements at each processor, routed these ps samples to a single processor, sorted them at that processor, and then selected every element as a splitter. Each processor then performs a binary search on these splitters for each of its input values and then uses the results to route the values to the appropriate destination, after which local sorting is done to complete the sorting process. The first difficulty with this approach is the work involved in gathering and sorting the samples. A larger value of s results in better load balancing, but it also increases the overhead. The second difficulty is that no matter how the routing is scheduled, there exist inputs that give rise to large variations in the number of elements destined for different processors, and this in turn results in an inefficient use of the communication bandwidth. Moreover, such an irregular communication scheme cannot take advantage of the regular communication primitives proposed under the MPI standard [26]. The final difficulty with the original approach is that duplicate values are accommodated by tagging each item with a unique value [10]. This, of course, doubles the cost of both memory access and interprocessor communication.

In our solution, we incur no overhead in obtaining samples from each processor and in sorting these samples to identify the splitters. Because of this very high oversampling, we are able to replace the irregular routing with exactly two calls to our transpose primitive, and, in addition, we are able to efficiently accommodate the presence of duplicates without resorting to tagging.

The pseudocode for our algorithm is as follows:

• Step (1): Each processor randomly assigns each of its elements to one of p buckets. With high probability, no bucket will receive more than elements, where is a constant to be defined later.
• Step (2): Each processor routes the contents of bucket j to processor , for . Since with high probability no bucket will receive more than elements, this is equivalent to performing a transpose operation with block size .
• Step (3): Each processor sorts at most values received in Step (2) using an appropriate sequential sorting algorithm. For integers we use the radix sort algorithm, whereas for floating point numbers we use the merge sort algorithm.
• Step (4): From its sorted list of elements, processor selects each element as , for . By default, is the largest value allowed by the data type used. Additionally, for each , binary search is used to determine the values and , which are respectively the fractions of the total number of elements at processor with the same value as and which also lie between index and index , inclusively.
• Step (5): Processor broadcasts the Splitter, , and arrays to the other p - 1 processors.
• Step (6): Each processor uses binary search on its sorted local array to define for each of the p splitters a subsequence . The subsequence associated with contains all those values which are greater than and less than , as well as and of the total number of elements in the local array with the same value as and , respectively.
• Step (7): Each processor routes the subsequence associated with to processor , for . Since with high probability no sequence will contain more than elements, where is a constant to be defined later, this is equivalent to performing a transpose operation with block size .
• Step (8): Each processor merges the p sorted subsequences received in Step (7) to produce the column of the sorted array. Note that, with high probability, no processor has received more than elements, where is a constant to be defined later.

We can establish the complexity of this algorithm with high probability - that is with probability for some positive constant . But before doing this, we need to establish the results of the following lemmas.

Lemma 1: At the completion of Step (1), the number of elements in each bucket is at most with high probability, for any and .

Proof: The probability that exactly elements are placed in a particular bucket in Step (1) is given by the binomial distribution

where , , and . Using the following Chernoff bound [12] for estimating the tail of a binomial distribution

the probability that a particular bucket will contain at least elements can be bounded by

Hence, the probability that any of the buckets contains at least elements can be bounded by

and Lemma 1 follows.

Lemma 2: At the completion of Step (2), the total number of elements received by processor , which comprise the set of samples from which the splitters are chosen, is at most with high probability, for any and .

Proof: The probability that processor receives exactly elements is given by the binomial distribution . Using the Chernoff bound for estimating the tail of a binomial distribution, the probability that processor receives at least elements can be bounded by and Lemma 2 follows.

Lemma 3: For each , where , let and be respectively the sets of input elements and samples that are both equal in value to , and let . Then, with high probability, no will contain more than elements, where

Proof: The set of input elements = can have more than members only if or less members are selected to be samples from the set = , which is the set composed of the first members in . However, since each element of is independently chosen to be a sample with probability , the probability of this event occurring is given by

Using the following ``Chernoff'' type bound [18] for estimating the head of a binomial distribution

where , , and , it follows that the probability that a set among the p sets of input elements has more than is bounded by

Using the fact that , it is easy to show that the above sum can be bounded by , for some and

The bound of Lemma 3 will also hold if we include the subsets of elements and samples whose values fall strictly between two consecutive splitters.

Lemma 4: At the completion of Step (7), the number of elements received by each processor is at most with high probability, for any ( without duplicates) and .

Proof: Let Q be the set of input elements to be sorted by our algorithm, let R be the set of samples of Step (4) at processor with cardinality , and and let S be the subset of R associated with , which we define to be the samples in R with indices through , inclusively. Let , , and be respectively the number of elements in Q, R, and S with value equal to , let , , and be respectively the number of elements in Q, R, and S with values greater than but less than , and let , , and be respectively the number of elements in Q, R, and S with value equal to .

According to Step (6) of our algorithm, processor will receive

elements. To compute the upper bound on this expression, we first use Lemma 3 to bound each , giving us

Rearranging this expression, we get:

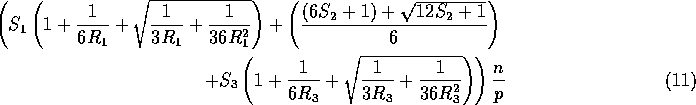
Clearly, this expression is maximized for and . Substituting these values and rearranging once again, we get:

Since , this expression is maximized for Since Lemma 2 guarantees that with high probability , Lemma 4 follows with high probability for . Alternatively, if there are no duplicates, we can show that the bound follows with high probability for .

Lemma 5: If the set of input elements is arbitrarily partitioned into at most 2p subsets, each of size , with high probability at the conclusion of Step (2) no processor will receive more than elements from any particular subset, for and .

Proof: The probability that exactly elements are sent to a particular processor by the conclusion of Step (2) is given by the binomial distribution . Using the Chernoff bound for estimating the tail of a binomial distribution, the probability that from M possible subsets any processor will receive at least elements can be bounded by

and Lemma 5 follows for .

Lemma 6: The number of elements exchanged by any two processors in Step (7) is at most with high probability, for any ( without duplicates) and .

Proof: Let U be the set of input elements to be sorted by our algorithm, let V be the set of elements held by intermediate processor after Step (2), and let W be the set of elements held by destination processor after Step (7). Let , , and be respectively the number of elements in U, V, and W with values equal to , let , , and be respectively the number of elements in U, V, and W with values greater than but less than , and let , , and be respectively the number of elements in U, V, and W with values equal to .

According to Step (6) of our algorithm, intermediate processor will send

elements to processor . To compute the upper bound on this expression, we first use Lemma 5 to bound each , giving us:

Notice that since destination processor receives respectively and of the elements at each intermediate processor with values equal to and , it follows that and . Hence, we can rewrite the expression above as

Rearranging this expression, we get:

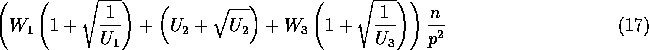
Clearly, this expression is maximized for and . Substituting these values and rearranging, we get:

Since , this expression is maximized for Since Lemma 4 guarantees that with high probability , Lemma 6 follows with high probability for . Alternatively, if there are no duplicates, we can show that the bound follows with high probability for .

With these bounds on the values of , , and , the analysis of our sample sort algorithm is as follows. Steps (1), (3), (4), (6), and (8) involve no communication and are dominated by the cost of the sequential sorting in Step (3) and the merging in Step (8). Sorting integers using radix sort requires time, whereas sorting floating point numbers using merge sort requires time. Step (8) requires time if we merge the sorted subsequences in a binary tree fashion. Steps (2), (5), and (7) call the communication primitives transpose, bcast, and transpose, respectively. The analysis of these primitives in [6] shows that with high probability these three steps require , , and , respectively. Hence, with high probability, the overall complexity of our sample sort algorithm is given (for floating point numbers) by

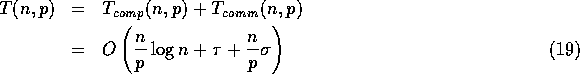
for .

Clearly, our algorithm is asymptotically optimal with very small coefficients. But a theoretical comparison of our running time with previous sorting algorithms is difficult, since there is no consensus on how to model the cost of the irregular communication used by the most efficient algorithms. Hence, it is very important to perform an empirical evaluation of an algorithm using a wide variety of benchmarks, as we will do next.